A continuous outcome takes a value that ranges between negative and positive infinity in theory. An example is the change in PSA level 3 months after drug administration in a prostate cancer trial. For continuous outcome, the goal is to determine if there is a difference in outcome means between the arms. To determine the number of patients in the trial, the investigator must first specify the expected means in the control and treatment arms, given by μ_c and μ_t respectively. The standard deviation of the outcome in the control group is denoted by σ. Using this notation, the required sample size is calculated based on testing the hypothesis
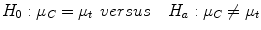such that the probability of a false positive is α and the power to detect the largest clinically relevant difference in means is 1 − β. Assuming that both the treatment and control arms consist of independent groups of patients and the standard deviation of the outcome in the control arm is similar to that in the treatment arm, a two-sample t-test is often used to test the above hypothesis. Based on this test, the required sample size for each arm is given by
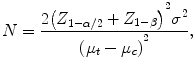where Z _q is the qth quantile of the standard normal distribution. Note that this formula is suitable for a relatively large N, but may not apply for small sample sizes.

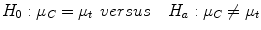
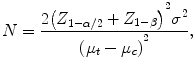
As an example, the outcome is the change of glomerular filtration rate (GFR) after 5 years in a kidney trial. Suppose that the change (decline) of GFR is 10 ml/min/1.73 m² in the control arm, with a standard deviation of 20. It is of clinical interest to detect a 5 ml/min/1.73 m² decline in the new treatment with 90 % power. The investigator would also like to ensure that the probability of a false positive is 5 %. Using the above formula, each arm of the study requires 337 patients.

A survival outcome, or more generally a time-to-event outcome, measures the time to the occurrence of certain clinical events in patients from their enrollment into the trial. In most cancer clinical trials, the primary outcome is patient survival, that is, time to mortality, and the most common objective is to evaluate the effect of a new treatment on prolonging patient survival.

Survival outcomes are usually subject to censoring. For patients who are alive at the end of the trial or lost to follow-up during the trial course, their exact deceased times are unknown but larger than the last follow-up time. The analysis of survival outcomes in a clinical trial is typically to compare hazard rates or median survival times between treatment arms. Hazard is the risk of developing the event at an instant in time, and median survival time is the time at which half of the patients are event-free. These two parameters are equivalent when the survival curve follows an exponential shape. Furthermore, the hazard ratio between two treatment arms may be constant over time, leading to the so called proportional hazards. Thus, without loss of generality, we focus on the sample size calculation for comparing hazard rates.