Physical Principles of Ultrasound

Fig. 2.1

Behavior of mechanical waves. Longitudinal waves oscillate parallel to the direction of propagation; transverse waves oscillate perpendicular to the direction of propagation

Frequency is the number of times per second the wave is repeated, measured in cycles/second (Hz). The human ear can hear frequencies ranging from 20 to 20,000 Hz. Ultrasound, by definition, refers to frequencies greater than 20,000 Hz. The frequencies most often utilized in medical ultrasound imaging are between 2 and 20 million cycles/second (MHz).

Wavelength is defined as the distance covered by one complete cycle (measured from peak to peak or trough to trough) and is typically measured in millimeters (Fig. 2.2). Wavelength, λ, is inversely proportional to the frequency, ƒ, and directly proportional to the propagation velocity, v, or speed at which a wave is traveling through a particular medium:

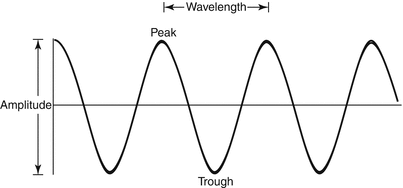
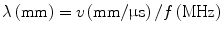
Fig. 2.2

Schematic representation of the properties of acoustic waves. See text for details

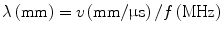
$\lambda \left(\mathrm{mm}\right)= v\left(\mathrm{mm}/\upmu \mathrm{s}\right)/ f\left(\mathrm{MHz}\right)$

The ability to distinguish objects along a sound beam depends on the wavelength of sound; one cannot differentiate objects whose dimensions are smaller than the wavelength of the incident wave. Thus, the higher the incident frequency, the greater the resolution of the image. As will be discussed shortly, better resolution attained with higher frequency comes at the cost of higher attenuation or loss of energy.

The amplitude of an acoustic wave represents the magnitude of the pressure in the medium as the wave travels (Fig. 2.2). The pressure is positive during the compression stage of the propagation and negative during the rarefaction stage. The logarithm of the square of the amplitude is measured in decibels (dB). Power is the amount of energy generated per unit time and is measured in joule/s or watts, where 0 dB (where decibel is a logarithmic unit expressing a quantity in relation to a reference level; in acoustics, it measures the intensity of sound pressure referred to a baseline pressure of 20 micropascals, commonly abbreviated as dB) refers to 1 milliwatt (mW). A 3 dB increase represents roughly doubling of power, which means that 3 dBm (where dBm is the power ratio in decibels (dB) of the measured power with a reference level of 1 mW) is equal to about 2 mW. For a 3 dB decrease, the power is reduced by half, making 3 dBm equal to about 0.5 mW. Intensity is the power density within an area and is expressed in W/m². Power and intensity describe the incident acoustic wave; gain refers to amplification of the returning echoes.

Tissue density and compressibility determine propagation velocity, which is a property of the medium through which sound travels. Higher density (mass/volume, measured in kg/m³) and/or lower compressibility results in a faster speed of sound. More dense solids, therefore, have a faster propagation velocity than air. In soft tissue, propagation velocity is relatively constant at 1,540 m/s; this is the value assumed by ultrasound machines for all human tissue. Additional velocities through various media are listed in Table 2.1.

Table 2.1

Propagation velocity of sound through various biologic media

Medium	Speed of sound (m/s)
Air	330
Fat	1,460
Water	1,480
Brain	1,540
Kidney	1,560
Liver	1,580
Blood	1,580
Muscle	1,580
Eye lens	1,640
Bone	3,000–4,500

Attenuation

As a sound wave propagates through a medium, some of the acoustic energy is “lost” or transformed into other forms of energy. This phenomenon is known as attenuation. Attenuation limits the depth of interrogation of a given frequency of the ultrasound beam, referred to as the penetration depth.

The attenuation of sound starts as soon as an electric pulse is converted to acoustic energy within the transducer and continues until the echo returns to the transducer to be processed into the image. Various factors contribute to attenuation including wavelength of the emitted sound, inherent properties of the medium, the number of interfaces encountered, and distance traveled. Attenuation is measured in decibels (dB), and the total attenuation in a specific medium is described by the “half-value thickness,” which is the distance within the medium at which the intensity of the beam is reduced to half. In soft tissue, acoustic energy is lost at a rate of approximately 0.5 dB/cm/MHz. Homogeneous tissue, with similar density throughout, will have a decreased rate of attenuation versus tissue with varying densities (heterogeneous). Simple fluid, such as water and saline or serous fluid, will have nearly null attenuation.

To understand attenuation one must analyze the behavior of the wave as it travels through a medium with various interfaces (Fig. 2.3). Reflection is the redirection of part of the sound wave back to its source caused by the incident wave striking an interface; this serves as the basis for creation of the ultrasound image. Ideally, the ultrasound beam should evaluate the anatomy of interest at 90° incidence to maximize the reflection and visualization of anatomic structures. Absorption, refraction, scattering, and diffraction all lead to attenuation of ultrasound energy.

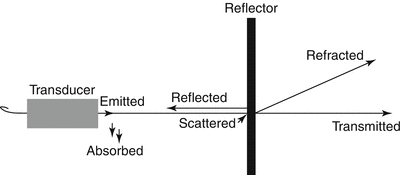
Fig. 2.3

Behavior of an acoustic wave as it travels through a medium

A wave hitting the interface at an angle less than 90° results in refraction of the wave away from the transducer at an angle equal to the angle of incidence but in the opposite direction (angle of reflection). When this happens, some of the returning echo is lost or attenuated. Diffuse reflection, or scattering, occurs where the dimensions of the interface are smaller than the acoustic wavelength, such as red blood cells or ultrasound contrast media. Depending on the size, shape, and orientation of the scatterers, scattering can redirect energy in all directions, or it can redirect energy primarily in the same direction as the incident energy, known as forward scattering, or in the reverse direction, known as backscattering. When received echoes are “translated” into ultrasound images, these different types of reflection result in different types of images.

Absorption, generally accepted as thermal losses, depends on the viscosity of the medium as well as the incident energy. This is generally a minor effect at diagnostic ultrasound intensities but is central in many therapeutic ultrasound applications.

As stated above inherent properties of the medium influence attenuation. The degree to which a medium slows sound wave propagation is known as acoustic impedance and is defined as

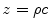$z=\rho c$

where z is acoustic impedance, ρ is the density of the material, and c is the sound velocity in that medium. The larger the difference in acoustic impedance between adjacent media (acoustic impedance mismatch), the more energy is lost as attenuation. Refraction is the redirection of part of the sound wave as it crosses a boundary of mediums with different acoustic impedances. Fortunately, the difference between the acoustic impedances of biologic tissues is very small, allowing for the creation of an ultrasound image without losing much to refraction.

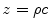
Each of these attenuation phenomena is influenced by the frequency of the transmitted wave. The higher the frequency, the greater the energy loss or attenuation. In the application of medical ultrasound, this influences your choice of transducer; although a higher frequency of sound would result in higher resolution, this is limited by the attenuation of the sound wave. In other words, you would use a lower-frequency transducer to reach deeper structures (at the sacrifice of image clarity) and a higher-frequency transducer for more superficial structures (to optimize clarity).

Resolution

Resolution may be further categorized into spatial (lateral and axial), temporal, and contrast resolution. In order to gain a better understanding of resolution, it is important to understand the anatomy of an ultrasound beam (Fig. 2.4). An ultrasound beam consists of two regions: the near field or Fresnel zone and the far field or Fraunhofer zone. The near field is adjacent to the transducer face and has a converging beam profile; this results in complex interference patterns close to the face, which can distort the ultrasound image. The far field or Fraunhofer zone is characterized by beam divergence and loss of ultrasound intensity. The point of transition between these two zones is the location of the maximum signal intensity (also known as the spatial peak intensity), and the distance from the transducer face to this point is known as the focal distance. The focal zone is defined as the region over which the width of the beam is less than two times the width of the focal distance. The focal zone can be manipulated by focusing the beam with a lens or with electronic directional manipulation of the transducer.